Counting Sheets is More Complex than it Seems — On Origami Classification, Part II
This post is part of a series on origami classification: Part I, Part II
In Part I of this series, I introduced the problem of origami classification and the shortcomings of some currently used approaches. Then, I proposed some guidelines upon which a possibly better system could be built. In this part, I will take a closer look at one of the most basic dimensions along which origami can be classified: the number of sheets.
Modular origami


It is common to divide origami into single-sheet and modular models. While this solution is good enough for most cases, I think it is not always sufficient.
The term modular origami is used in different ways, and sometimes implies that units are identical, or at least very similar, or that the model represents an abstract geometric shape. Such definitions leave a number of designs, for example animals made from two sheets, in a gray area between single-sheet and modular.
So how do I understand modular origami? First off, I think the definition should only depend on the number of sheets, and not the subject. As mentioned in Part I of this series, I prefer to not mix different dimensions of the classification. Figurative modular origami is a thing, by the way.

As far as the number of units is concerned, some modulars are made of thousands of units while some are made from just two. I believe there is also such a thing as modulars made from a single unit. If a unit can in itself be treated as an interesting model, especially if it can connect to itself in a way identical to that used in larger assemblies, I think it is natural to treat such a design as being single-sheet and modular (with module count equal to one) at the same time. If a unit permits assemblies of 100, …, 10, …, 3, 2 and 1, I see no reason to treat the 1-unit assembly as a completely different genre. Since I like the novelty factor of such designs, I have created several, the first one being Single Module Modular Heart which is the single-unit special case of Heart-Shaped Coil.
Even if a unit does not connect to itself and a single piece is not very attention-worthy, modular origami units are certainly a kind of origami work, and usually designing the units is considered a greater accomplishment than just designing a model from previously known units. Technically, single units are usually single-sheet, but metamodules of multiple sheets are sometimes used as well. However, apart from the single-module modulars, individual units are normally treated as building blocks rather than complete models. Thus, it may be tempting to treat them as a separate category. However, this would mean mixing two separate dimensions: the number of sheets and the subject of the model. I would like my classification to encompass any folded piece(s) of paper, regardless of whether it “looks nice” or is something a designer would consider a finished work. The difference between modular origami units and other single-sheet designs stems only from function and not from the number of sheets. Thus, single units end up in the intersection between single-sheet and modular types in my system. The difference between a single unit and a single-unit modular (if one can be built from that unit) lies only in locking the unit with itself, which I consider a kind of shaping, and thus not a separate design.
Compound origami

I think that designs which use multiple sheets but each one folded in a significantly different way, should be treated as a category separate from modular origami. Of course, there are corner cases such as my Python Logo II, where one wonders if the difference between the way different sheets are folded is big enough, but I think there is a significant structural difference between a two-sheet model such as the traditional ninja star whose both sheets are folded the same way (except for mirror symmetry) and a two-sheet animal where one sheet represents the head and the other the rest of the body, both folded in a completely different way (for an abstract example, see my Maltese Cross Framed).
I originally used the term non-modular multi-sheet for such designs until David Mitchell made me aware of the term compound origami which is also sufficiently unambiguous but so much more elegant.
Compositions


One more type of models which I think deserves a category of its own but doesn’t seem to get much press is what I call Compositions. An example would be a scene composed of several disparate models, for example representing a few animals and some buildings. The reason I think such a scene should be treated as a separate origami design, belonging to a new category, is that the whole is more than just the sum of its parts. Some people create complete dioramas with quite complex scenery this way, and I believe that the composition brings more to the table than if we considered each of the constituent parts separately.
I think this is in a way similar to the relationship between a modular origami unit and the different models which can be built from that unit. Sure, designing the unit is in many ways more creative than just taking an existing unit and building a new model out of it, but people often find new and unexpected ways of using existing units, and I think this deserves some credit as well. Actually, I tend to think of the Composition-type models as being “like modulars, but not connected”. Models such as my Crystal Structure of Gibbsite are just that: a regular arrangement of identical elements, but these elements (accidentally, modular origami by themselves in this case) are not joined and will fall apart if you move them from the table where the were laid out. In the general case, the elements of a composition do not have to be identical, and can even be of different types with regard to the number of sheets as is the case for Ad Astra.
Some compositions can be partially connected, not necessarily by means of origami. Therefore, I would also count things such as the Senbazuru (a thousand origami cranes, possibly connected by strings) or traditional kusudamas (folded flowers connected into a ball with glue or string) into this category. Models traditionally considered modular, whose connections are weak and need glue to hold the model together (as is the case with some kusudamas), would also fall into the composition category in my system. Of course, there exist corner cases.
It might be debatable how much “value added” the combination of multiple models needs to provide compared to the same models considered separately in order to become a composition. For simplicity, I assume there is no threshold, and any setup of multiple models can be considered a composition. Thus, at an origami exhibition at a convention, where many tables full of models are displayed, we are dealing with a huge number of compositions, many of which were never planned by the people who put their models on display there. Perhaps we should call such unintended compositions which arise spontaneously virtual compositions just like we speak of virtual particles in physics.
Anything more?
Do the types mentioned above cover all possibilities (within the factors taken into account here, of course)? The discussion could be summarized as the following Cartesian product: {one sheet, multiple sheets} × {similar, dissimilar} × {connected, not connected}. This means, in theory, a total of eight possible triples: (one sheet, similar, connected), (one sheet, similar, disconnected), …, (multiple sheets, dissimilar, not connected). Clearly, for one sheet, it makes no sense to distinguish between similar and dissimilar sheets, and between connected and not connected. This gives us just one type for single-sheet models. For multi-sheet models, there are four possibilities: (similar, connected) — which is the modular type, (dissimilar, connected) — which is the compound origami type, and two types of not connected models (similar and dissimilar elements). So, one can name two subtypes of the composition type: the modular composition (an example of which would be the Crystal Structure of Gibbsite) and the non-modular composition (for example Ad Astra).
The composition being modular or non-modular is a question separate from the one whether individual elements that make up the composition are modular or not. For example, the Senbazuru is a modular composition since all elements are identical, even though the elements (traditional cranes) are not modular. In practice, the distinction between modular and non-modular compositions may be excessively fine-grained and unnecessary in most cases.
The single-module modular is a special case: a generic design which can be made of any or almost any number N of modules, for the special case of N = 1. One could apply the same logic to compositions, but it wouldn’t make much sense: the end result would be just a single-sheet design. For example, generalizing the Senbazuru as a design consisting of N cranes, for N = 1 we get a single crane which is just a single-sheet design. The difference between modulars and [modular] compositions lies in the fact of the modular being connected: it is the possibility of connecting a single unit to itself which allows the single-module modular to be a proper subset of single-sheet designs.
One weird model
Let’s consider my Fortune Teller Christmas Tree since I think it’s a neat accumulation of all sorts of corner cases. It’s a Christmas Tree made from several traditional Fortune Tellers stacked one on top of another and topped out with one custom module for the tip of the tree. This makes it:
- a figurative modular design (figurative and other subject matters will be the topic of another post)
- but the Fortune Tellers are different sizes, and one unit is completely different, so maybe it’s a compound origami design after all?
- if it’s to be considered a modular, the traditional Fortune Teller unexpectedly becomes a modular origami unit (it’s also been used as a modular by others, by the way)
- since the number of levels can be varied, and without the tip the tree is still a tree, a single Fortune Teller (a level-1 Christmas Tree without the tip) should be considered a single-module modular
- which would also mean that a Fortune Teller is a modular design (but single-sheet at the same time), and a figurative model at that since it’s a variant of the Christmas Tree
- there are no pockets or other locking mechanism: individual Fortune Tellers are held together only by gravity; so maybe it’s a composition rather than a modular or compound design? does a model’s classification with regard to the number of sheets change when we move it from Earth to a low-gravity environment in Earth’s orbit?
The answers to these questions are left as an exercise to the reader. These conclusions seem weird, but maybe it’s just because we are not used to comprehensively analyzing the classification of origami models and its consequences.
Summary
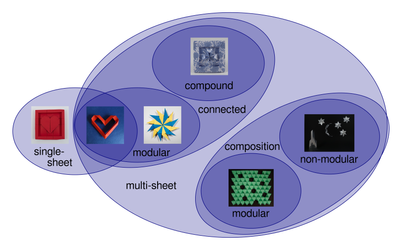
In the end, this discussion leads to the following classification of origami in the dimension of the number of sheets:
- single-sheet
- multi-sheet
- connected
- composition (not fully connected)
- modular
- non-modular
Comments